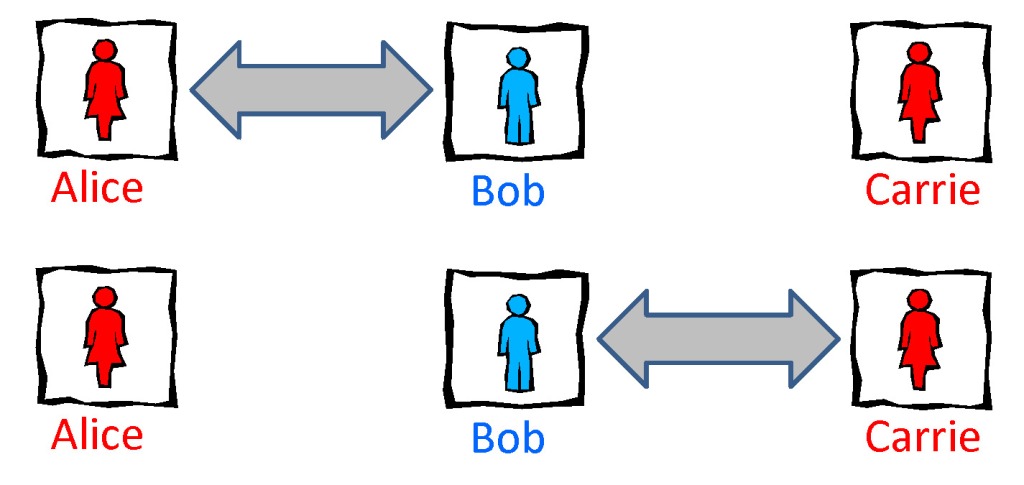
Quantum correlations are monogamous. Bob can be highly entangled with Alice or with Carrie, but not both.
Back in the early 1990s, I was very interested in the quantum physics of black holes and devoted much of my research effort to thinking about how black holes process quantum information. That effort may have prepared me to appreciate Peter Shor’s spectacular breakthrough — the discovery of a quantum algorithm for factoring intergers efficiently. I told the story here of how I secretly struggled to understand Shor’s algorithm while attending a workshop on black holes in 1994.
Since the mid-1990s, quantum information has been the main focus of my research. I hope that some of the work I’ve done can help to hasten the onset of a new era in which quantum computers are used routinely to perform super-classical tasks. But I have always had another motivation for working on quantum information science — a conviction that insights gained by thinking about quantum computation can illuminate deep issues in other areas of physics, especially quantum condensed matter and quantum gravity. In recent years quantum information concepts have begun penetrating into other fields, and I expect that trend to continue.
The study of quantum black holes has continued to be a very active and fruitful research area in recent years. I’ve not been much involved myself, though, except for one foray (well, also this one). But my friend Lenny Susskind encouraged me to attend a workshop on black holes at Stanford this past weekend, and I’m glad I did. It was fun, and it was gratifying to see that quantum information concepts were prominently featured in many of the talks.
The goal of the workshop was to clarify a question raised in this paper by Almheiri, Marolf, Polchinski, and Sully (AMPS): if a black hole is highly entangled with its surroundings, does a freely falling observer who crosses the event horizon burn to a crisp immediately right at the horizon. We have always believed that if Alice foolishly enters a black hole she will be just fine for a while, but will gradually encounter stronger and stronger gravitational forces which will eventually tear her to pieces. AMPS argued that under the right circumstances, Alice’s horrible death comes much earlier than expected, and without any warning. Joe Polchinski wrote a nice explanation of the AMPS argument over at Cosmic Variance, but I’ll give my own version here.
To understand the AMPS puzzle, one needs to appreciate that quantum correlations are different than classical correlations. Classical correlations can be “polygamous” while quantum correlations are “monogamous.”
If Alice and Bob both have copies of the same newspaper, then Alice and Bob become correlated because both can access the same information. But Carrie can acquire a copy of that same newspaper; Bob’s correlation with Alice does not prevent him from becoming just as strongly correlated with Carrie. For that matter, anyone else can buy a newspaper to join the party.
A quantum newspaper is different, because you can read it in two (or more) complementary ways, and we say that two newspapers are “maximally entangled” (have the strongest possible quantum correlations) if both newspapers have the same content when both are read in the same way. In that case, if Alice reads her paper held right-side up she finds only random gibberish, but if Bob reads his newspaper right-side up he sees exactly the same gibberish as Alice. If on the other hand Alice had chosen to read the paper turned sideways, she would have found some other random gibberish, but again Bob would see the same gibberish as Alice if he read his paper sideways, too. Because there is just one way to read a classical newspaper, and lots of ways to read a quantum newspaper, the quantum correlations are stronger than classical ones.
So strong, in fact, that Bob’s entanglement with Alice limits his ability to entangle with Carrie. Bob’s entropy S(B), a measure of his capacity to entangle with others, is an upper bound on the sum of Bob’s entanglement E(A,B) with Alice and his entanglement E(B,C) with Carrie. If Bob is highly entangled with Alice then he can entangle with Carrie only by sacrificing some of his entanglement with Alice. That’s why we say that entanglement is monogamous.
Following AMPS, imagine a black hole which is maximally entangled with another quantum system C outside the black hole. Like any black hole, this one evaporates by emitting Hawking radiation. Also following AMPS, assume that the evaporation is unitary, i.e., conserves quantum information. There is strong evidence that unitarity is an inviolable principle of physics, and we don’t really know how to make sense of quantum mechanics without it. Unitarity implies that as a system B is emitted by the black hole in the form of Hawking radiation, this system B, like the black hole from which it emerged, must be maximally entanged with C. And monogamy of entanglement means that B cannot be entangled with anything else besides C.
But this spells trouble for Alice, the brave soul who dares to fall into the black hole. If Alice’s passage through the event horizon were uneventful then she would fall though space that is nearly devoid of particles. But if we cut the empty space seen by Alice into the inside and outside of the black hole at the event horizon, then the particles in system B seen by an observer who stays outside are paired with particles on the inside — B is entangled with a system A inside the horizon, violating the monogamy of entanglement. Something’s wrong.
The AMPS proposal is that what Alice encounters at the horizon does not look like empty space at all — rather B and A are unentangled, which means that Alice sees many energetic particles. Monogamy of entanglement is rescued, but not poor Alice. She is incinerated by an intense wall of fire as she attempts to pass through the event horizon.
If a black hole forms from a collapsing star and then radiates for a long, long, long time until it has shed more than half its initial entropy, we expect the black hole to become maximally entangled with the radiation already emitted, and hence (if AMPS are right) for a firewall to appear. It is as though the singularity, which we expected to find deep inside the black hole, has crept right up to the event horizon when the black hole is very old.
Like many other physicists, I distrust this conclusion. The black hole could be very large, so that as Alice approaches the horizon she experiences only very weak tidal gravitational forces. It seems terribly unjust for Alice, unaware of the black hole’s age and with no indication that anything is amiss, to suddenly fry without any warning at all.
My first reaction to the AMPS paper was that we should think very carefully about whether, if there are no firewalls, the putative violation of monogamy of entanglement really has a clear operational meaning. We might be willing to tolerate polygamous entanglement if no observer can ever detect the crime! We must ask whether it is possible, at least in principle, for Alice to verify the entanglement between B and C, and then test the entanglement between B and A by plunging into the black hole. AMPS discuss this issue in their paper, but I don’t consider it to be settled. One consideration, mentioned at the workshop by both Patrick Hayden and Daniel Harlow, is that verifying the BC entanglement requires a quantum computation that might be infeasible as a matter of principle, at least for a large black hole.
For now, it seems appropriate to assume both information conservation and no firewalls, seeking some way of reconciling the two. This might involve truly radical revisions in the foundations of quantum mechanics, or bizarre nonlocal dynamics outside the black hole. If we are forced to accept that firewalls really exist, then we will need a deeper understanding of their dynamical origin than the indirect argument AMPS provided.
The workshop was invigorating because nearly everyone seemed confused. Paradoxes are always welcome in physics, as they can help to point us toward revolutionary advances. While no consensus has yet emerged about what the AMPS puzzle is teaching us, I’m hoping that the outcome will be a big stride forward in our understanding of quantum information in gravitational systems.
