I am a theoretical physicist at University of California, Berkeley. Last month, I attended a very interesting conference organized by Foundamental Questions Institute (FQXi) in Puerto Rico, and presented a talk about making predictions in cosmology, especially in the eternally inflating multiverse. I very much enjoyed discussions with people at the conference, where I was invited to post a non-technical account of the issue as well as my own view of it. So here I am.
I find it quite remarkable that some of us in the physics community are thinking with some “confidence” that we live in the multiverse, more specifically one of the many universes in which low-energy physical laws take different forms. (For example, these universes have different elementary particles with different properties, possibly different spacetime dimensions, and so on.) This idea of the multiverse, as we currently think, is not simply a result of random imagination by theorists, but is based on several pieces of observational and theoretical evidence.
Observationally, we have learned more and more that we live in a highly special universe—it seems that the “physical laws” of our universe (summarized in the form of standard models of particle physics and cosmology) takes such a special form that if its structure were varied slightly, then there would be no interesting structure in the universe, let alone intelligent life. It is hard to understand this fact unless there are many universes with varying “physical laws,” and we simply happen to emerge in a universe which allows for intelligent life to develop (which seems to require special conditions). With multiple universes, we can understand the “specialness” of our universe precisely as we understand the “specialness” of our planet Earth (e.g. the ideal distance from the sun), which is only one of the many planets out there.
Perhaps more nontrivial is the fact that our current theory of fundamental physics leads to this picture of the multiverse in a very natural way. Imagine that at some point in the history of the universe, space is exponentially expanding. This expansion—called inflation—occurs when space is filled with a “positive vacuum energy” (which happens quite generally). We knew, already in 80’s, that such inflation is generically eternal. During inflation, various non-inflating regions called bubble universes—of which our own universe could be one—may form, much like bubbles in boiling water. Since ambient space expands exponentially, however, these bubbles do not percolate; rather, the process of creating bubble universes lasts forever in an eternally inflating background. Now, recent progress in string theory suggests that low energy theories describing phyics in these bubble universes (such as the elementary particle content and their properties) may differ bubble by bubble. This is precisely the setup needed to understand the “specialness” of our universe because of the selection effect associated with our own existence, as described above.

A schematic depiction of the eternally inflating multiverse. The horizontal and vertical directions correspond to spatial and time directions, respectively, and various regions with the inverted triangle or argyle shape represent different universes. While regions closer to the upper edge of the diagram look smaller, it is an artifact of the rescaling made to fit the large spacetime into a finite drawing—the fractal structure near the upper edge actually corresponds to an infinite number of large universes.
This particular version of the multiverse—called the eternally inflating multiverse—is very attractive. It is theoretically motivated and has a potential to explain various features seen in our universe. The eternal nature of inflation, however, causes a serious issue of predictivity. Because the process of creating bubble universes occurs infinitely many times, “In an eternally inflating universe, anything that can happen will happen; in fact, it will happen an infinite number of times,” as phrased in an article by Alan Guth. Suppose we want to calculate the relative probability for (any) events $latex A$ and $latex B$ to happen in the multiverse. Following the standard notion of probability, we might define it as the ratio of the numbers of times events $latex A$ and $latex B$ happen throughout the whole spacetime
$latex P = frac{N_A}{N_B}$.
In the eternally inflating multiverse, however, both $latex A$ and $latex B$ occur infinitely many times: $latex N_A, N_B = infty$. This expression, therefore, is ill-defined. One might think that this is merely a technical problem—we simply need to “regularize” to make both $latex N_{A,B}$ finite, at a middle stage of the calculation, and then we get a well-defined answer. This is, however, not the case. One finds that depending on the details of this regularization procedure, one can obtain any “prediction” one wants, and there is no a priori preferred way to proceed over others—predictivity of physical theory seems lost!
Over the past decades, some physicists and cosmologists have been thinking about many aspects of this so-called measure problem in eternal inflation. (There are indeed many aspects to the problem, and I’m omitting most of them in my simplified presentation above.) Many of the people who contributed were in the session at the conference, including Aguirre, Albrecht, Bousso, Carroll, Guth, Page, Tegmark, and Vilenkin. My own view, which I think is shared by some others, is that this problem offers a window into deep issues associated with spacetime and gravity. In my 2011 paper I suggested that quantum mechanics plays a crucial role in understanding the multiverse, even at the largest distance scales. (A similar idea was also discussed here around the same time.) In particular, I argued that the eternally inflating multiverse and quantum mechanical many worlds a la Everett are the same concept:
Multiverse = Quantum Many Worlds
in a specific, and literal, sense. In this picture, the global spacetime of general relativity appears only as a derived concept at the cost of overcounting true degrees of freedom; in particular, infinitely large space associated with eternal inflation is a sort of “illusion.” A “true” description of the multiverse must be “intrinsically” probabilistic in a quantum mechanical sense—probabilities in cosmology and quantum measurements have the same origin.
To illustrate the basic idea, let us first consider an (apparently unrelated) system with a black hole. Suppose we drop some book $latex A$ into the black hole and observe subsequent evolution of the system from a distance. The book will be absorbed into (the horizon of) the black hole, which will then eventually evaporate, leaving Hawking radiation. Now, let us consider another process of dropping a different book $latex B$, instead of $latex A$, and see what happens. The subsequent evolution in this case is similar to the case with $latex A$, and we will be left with Hawking radiation. However, this final-state Hawking radiation arising from $latex B$ is (believed by many to be) different from that arising from $latex A$ in its subtle quantum correlation structure, so that if we have perfect knowledge about the final-state radiation then we can reconstruct what the original book was. This property is called unitarity and is considered to provide the correct picture for black hole dynamics, based on recent theoretical progress. To recap, the information about the original book will not be lost—it will simply be distributed in final-state Hawking radiation in a highly scrambled form.
A puzzling thing occurs, however, if we observe the same phenomenon from the viewpoint of an observer who is falling into the black hole with a book. In this case, the equivalence principle says that the book does not feel gravity (except for the tidal force which is tiny for a large black hole), so it simply passes through the black hole horizon without any disruption. (Recently, this picture was challenged by the so-called firewall argument—the book might hit a collection of higher energy quanta called a firewall, rather than freely fall. Even if so, it does not affect our basic argument below.) This implies that all the information about the book (in fact, the book itself) will be inside the horizon at late times. On the other hand, we have just argued that from a distant observer’s point of view, the information will be outside—first on the horizon and then in Hawking radiation. Which is correct?
One might think that the information is simply duplicated: one copy inside and the other outside. This, however, cannot be the case. Quantum mechanics prohibits faithful copying of full quantum information, the so-called no-cloning theorem. Therefore, it seems that the two pictures by the two observers cannot both be correct.
The proposed solution to this puzzle is interesting—both pictures are correct, but not at the same time. The point is that one cannot be both a distant observer and a falling observer at the same time. If you are a distant observer, the information will be outside, and the interior spacetime must be viewed as non-existent since you can never access it even in principle (because of the existence of the horizon). On the other hand, if you are a falling observer, then you have the interior spacetime in which the information (the book itself) will fall, but this happens only at the cost of losing a part of spacetime in which Hawking radiation lies, which you can never access since you yourself are falling into the black hole. There is no inconsistency in either of these two pictures; only if you artificially “patch” the two pictures, which you cannot physically do, does the apparent inconsistency of information duplication occurs. This somewhat surprising aspect of a system with gravity is called black hole complementarity, pioneered by ‘t Hooft, Susskind, and their collaborators.
What does this discussion of black holes have to do with cosmology, and, in particular the eternally inflating multiverse? In cosmology our space is surrounded by a cosmological horizon. (For example, imagine that space is expanding exponentially; this makes it impossible for us to obtain any signal from regions farther than some distance because objects in these regions recede faster than speed of light. The definition of appropriate horizons in general cases is more subtle, but can be made.) The situation, therefore, is the “inside out” version of the black hole case viewed from a distant observer. As in the case of the black hole, quantum mechanics requires that spacetime on the other side of the horizon—in this case the exterior to the cosmological horizon—must be viewed as non-existent. (In the paper I made this claim based on some simple supportive calculations.) In a more technical term, a quantum state describing the system represents only the region within the horizon—there is no infinite space in any single, consistent description of the system!
If a quantum state represents only space within the horizon, then where is the multiverse, which we thought exists in an eternally inflating space further away from our own horizon? The answer is—probability! The process of creating bubble universes is a probabilistic process in the quantum mechanical sense—it occurs through quantum mechanical tunneling. This implies that, starting from some initially inflating space, we could end up with different universes probabilistically. All different universes—including our own—live in probability space. In a more technical term, a state representing eternally inflating space evolves into a superposition of terms—or branches—representing different universes, but with each of them representing only the region within its own horizon. Note that there is no concept of infinitely large space here, which led to the ill-definedness of probability. The picture of initially large multiverse, naively suggested by general relativity, appears only after “patching” pictures based on different branches together; but this vastly overcounts true degrees of freedom as was the case if we include both the interior spacetime and Hawking radiation in our description of a black hole.
The description of the multiverse presented here provides complete unification of the eternally inflating multiverse and the many worlds interpretation in quantum mechanics. Suppose the multiverse starts from some initial state $latex |Psi(t_0)rangle$. This state evolves into a superposition of states in which various bubble universes nucleate in various locations. As time passes, a state representing each universe further evolves into a superposition of states representing various possible cosmic histories, including different outcomes of “experiments” performed within that universe. (These “experiments” may, but need not, be scientific experiments—they can be any physical processes.) At late times, the multiverse state $latex |Psi(t)rangle$ will thus contain an enormous number of terms, each of which represents a possible world that may arise from $latex |Psi(t_0)rangle$ consistently with the laws of physics. Probabilities in cosmology and microscopic processes are then both given by quantum mechanical probabilities in the same manner. The multiverse and quantum many worlds are really the same thing—they simply refer to the same phenomenon occurring at (vastly) different scales.
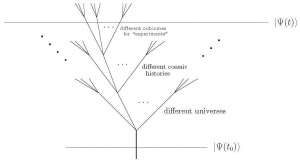
A schematic picture for the evolution of the multiverse state. As t increases, the state evolves into a superposition of states in which various bubble universes nucleate in various locations. Each of these states then evolves further into a superposition of states representing various possible cosmic histories, including different outcomes of experiments performed within that universe.
The picture presented here does not solve all the problems in eternally inflating cosmology. What is the actual quantum state of the multiverse? What is its “initial conditions”? What is time? How does it emerge? The picture, however, does provide a framework to address these further, deep questions, and I have recently made some progress: the basic idea is that the state of the multiverse (which may be selected uniquely by the normalizability condition) never changes, and yet time appears as an emergent concept locally in branches as physical correlations among objects (along the lines of an old idea by DeWitt). Given the length already, I will not elaborate on this new development here. If you are interested, you might want to read my paper.
It is fascinating that physicists can talk about big and deep questions like the ones discussed here based on concrete theoretical progress. Nobody really knows where these explorations will finally lead us to. It seems, however, clear that we live in an exciting era in which our scientific explorations reach beyond what we thought to be the entire physical world, our universe.
