Date: 8/22/2013
Location: Caltech Cryo Lab, West Bridge:
Hello: I am Steve Maloney, a Physics and Chemistry teacher intern from Duarte High School, sponsored by IQIM (Institute for Quantum Information and Matter), doing whatever I can to be of assistance to Dr. Nicolas Smith-Lefebvre. Upon meeting him in mid-June I soon learned that our mission for the length of my visit was to assist him in determining with a greater degree of certainty the linear expansion coefficient of silicon in and around 125 K. (See below)

Fig. 1: Silicon cavity.
The temperature of 125 K is of special interest to operators of LIGO (Laser Interferometer Gravitational Wave Observatory), because that is one of two temperatures where the thermal expansion coefficient, $latex alpha$, of silicon is equal to zero. A zero linear expansion coefficient is of special interest to LIGO researchers because a small change in temperature inside the cryostat, (see Fig. 2, below) will not result in a significant change in length for the silicon cavity shown in Fig. 1.

Fig. 2: Inside the Cryostat
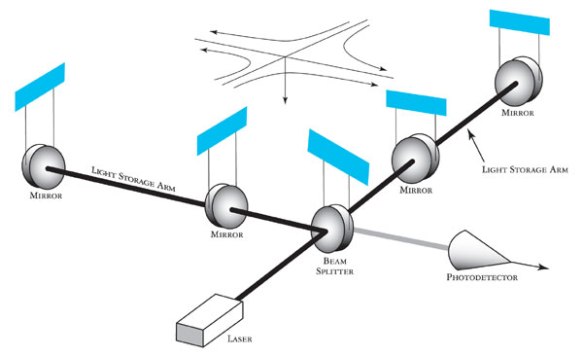
Scientists working at LIGO need to know with great precision the length of the resonance cavity, because as gravitational waves pass through the cavity, they simultaneously compress the length of the cavity and stretch in a direction perpendicular to the shortening (warp). The arrival of a gravity wave produces a signal in the Fabry-Perot Interferometer, shown in Fig. 3, below.
Because the interferometer is sensitive to changes in length of as little as 1X10-15 m, sources of noise must be reduced to an absolute minimum. This brings us back to establishing the Thermal Coefficient of Linear Expansion, $latex alpha$. Knowing the value of $latex alpha$ to a greater certainty will provide LIGO researchers the mathematical tools to better correct for small changes in temperature for the cavity, thus reducing the noise, therefore increasing the sensitivity of the Gravity Wave Detector.
So Where Do I Fit In?
In the Cryo-Lab on Thursday, July 11 2013, Nicolas Smith-Lefebvre, with my assistance, fed a radio frequency of 160.13 Mhz by means of a frequency-to-voltage transducer. The frequency fed into the transducer was changed by a fixed amount, and the change in voltage was noted. The hz / volt constant obtained was 253.9 hz / mvolt.
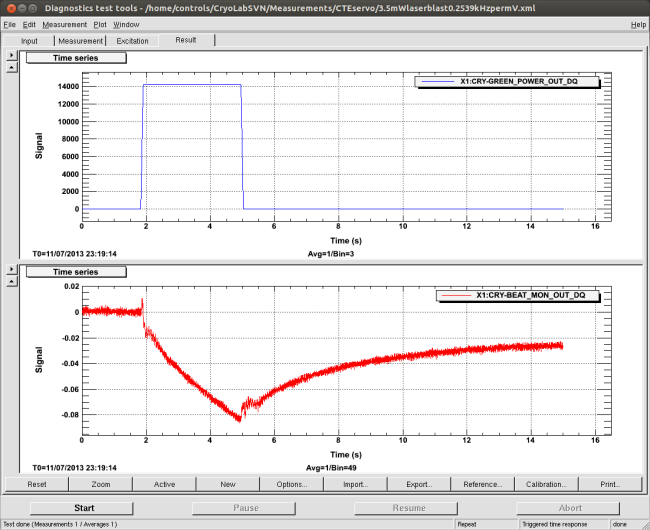
Nicolas then locked the east-west cryo-cavities so that the beat signal was approximately 0 (zero) volts. See the plot, below:
We then sent a 3.16 second pulse (approximated) of a 3.6 mWatt, 532 nm laser, (green) onto the surface of a mirror that reflects in the infrared, but absorbs in visible wavelengths. (Note top graph) I manufactured the electrical power interface for the laser by modifying the casing of a BIC disposable pen. The mirror was situated at the aperture of a silicon spacer.
The goal of the experiment was to determine the absorbance of the silicon mirror of the 532 nm laser.
Assuming we know the quantity of energy pulsed into the mirror:
3.6 mWatt * 3.16 s = .011376 joules,
the change in length of the cavity was determined by: Change in f/f1550nm = change in L/ L0
The change in volts (.025) gave us a change in f of 6.3475 x 103 hz.
With L0 having a value of 10 cm, that means change in L was 3.2794 x 10-10cm.
The specific heat capacity of Si is 700j/k*kg.
Coefficient of linear expansion for Si = 2.6 x 10 -6/K.
To calculate increase in temperature we need to obtain the change in L.
If 2.6 x 10 -6/C x 10 cm x DT = DL = 3.2794 x 10-10 cm, then DT must be 1.2613 x 10 -5 K.
If DT = 1.2613 x 10-5 K , then Q must equal .41 kg x 700 j/kg Kx1.2613 x 10-5 K = 3.6 x10-3 j,
Q/Epulse= 3.6 x 10-3j / 1.1376 x 10-2j = .316 absorbance.
In other words, the silicon cavity reflected about 68% of the light that struck it.
What have I come away with from this experience?
What struck me first and foremost during this summer internship in the Cryo-Lab was the importance of future knowledge workers of having certain key skills. Among them:
Proficiency in Language
Proficiency in Math
Proficiency in Science
Proficiency in Coding
I will share my insights with my local school district and I intend to capitalize on the connections I made during my experience at Caltech.
Acknowledgements:
I would like to thank the Duarte Unified School District for giving me a leave of absence, Rana Adhikari for, yet again, finding space for me in spite of my general ineptitude regarding General Relativity, Spyridon Michalakis (Spiros) for inviting me back and letting me participate in cutting-edge science, and most of all I would like to thank Nicolas Smith-Lefebvre (softball savant), and David Yeaton-Massey (D-Mass), for their patience, generosity, and mentoring.