A new paper by Nicole Yunger Halpern, Brian Swingle and Justin Dressel combines the out-of-time-ordered correlator (OTOC) and the Kirkwood-Dirac (KD) quasiprobability.
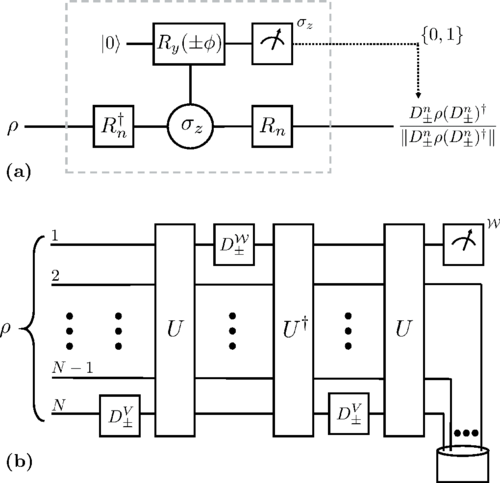
Quantum circuit for inferring the coarse-grained OTOC quasiprobability A from weak measurements. [Fig. 3]
This work not only illuminates the OTOC’s underpinnings, but also generalizes quasiprobability theory and motivates immediate-future weak-measurement challenges.
Read the full paper:




