Stabilizer codes are among the most successful quantum error-correcting codes, yet they have important limitations on their ability to fault tolerantly compute. In a recent paper by Sherman Fairchild Postdoctoral Scholar Tomas Jochym-O’Connor, IQIM alum Alex Kubica and Theodore Yoder introduce a new quantity, the disjointness of the stabilizer code, which, roughly speaking, is the number of mostly nonoverlapping representations of any given nontrivial logical Pauli operator.
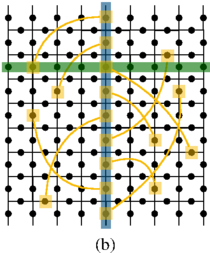
(b) For a given representative of ¯Z (blue) and any constant-depth circuit U with possibly geometrically nonlocal gates (depicted in yellow), one can always find a representative of ¯X (green), such that U¯ZU† and ¯X overlap only on a constant number of qubits.
The notion of disjointness proves useful in limiting transversal gates on any error-detecting stabilizer code to a finite level of the Clifford hierarchy. For code families, they can similarly restrict logical operators implemented by constant-depth circuits. For instance, they show that it is impossible, with a constant-depth but possibly geometrically nonlocal circuit, to implement a logical non-Clifford gate on the standard two-dimensional surface code.
Read the full paper: Tomas Jochym-O’Connor, Aleksander Kubica, and Theodore J. Yoder, Disjointness of Stabilizer Codes and Limitations on Fault-Tolerant Logical Gates, Phys. Rev. X 8, 021047 – Published 21 May 2018



