Classes
Classes and Notes
IQIM is training a new generation of leaders who will define the future of quantum science and engineering. Resources contributing to that development are included here.
APh 150: Introduction to Quantum Devices
Instructor: Oskar Painter
This class is meant to be an introduction to the quantum technologies currently being developed for the processing and communication of quantum information. Topics covered will include a primer on quantum computation (qubits, quantum gates, Shor’s algorithm, etc.) and quantum-limited measurement (shot noise, quantum-limited amplifiers, weak measurement, decoherence, etc.), atomic quantum optical memories, optomechanics, color centers, superconducting quantum circuits, and quantum plasmonics. Prerequisite: Ph 12 or equivalent.
Instructor: John Preskill
This two-term course covers quantum information theory, quantum algorithms, quantum error correction, quantum Shannon theory, and some special topics. The theory of quantum information and quantum computation. Overview of classical information theory, compression of quantum information, transmission of quantum information through noisy channels, quantum error-correcting codes, quantum cryptography and teleportation. Overview of classical complexity theory, quantum complexity, efficient quantum algorithms, fault-tolerant quantum computation, physical implementations of quantum computation. Prerequisites: Ph 125 abc or equivalent.
Please visit the course webpage, which includes links to class notes.
APh 250/ME 201 (Fall 2019): A numerical introduction to tensor networks for quantum simulation
Instructor: Austin Minnich
Tensor networks have emerged as a powerful tool for the numerical simulation of quantum many-body systems. This course will cover the fundamentals of tensor networks and recent algorithmic developments from a numerical perspective. Emphasis will be placed on both the theoretical foundation and practical numerical implementation of a variety of 1D and 2D tensor network algorithms. Specific topics to be covered include:
- Fundamentals of matrix product states, canonical forms, computation of expectation values, matrix product operators, and other basics
- Numerical renormalization group for impurity problems
- Density matrix renormalization group, including time-dependent and imaginary-time algorithms, and tangent space methods
- Pair-entangled projected states (PEPS), tensor network renormalization (TNR), 2D canonical forms, isometric PEPS, and fermionic PEPS.
Prerequisites: Ph 125, Ch 125, or equivalent graduate quantum mechanics course. ACM 104 or equivalent linear algebra course.
Instructor: Austin Minnich
Quantum computers with tens of physical qubits and high gate fidelities will become available in the next few years. This class will explore how this new type of computing device could be used to address research questions in physics. Specific topics to be covered include:
- Fundamentals of quantum computing and key algorithms
- Translating states and Hamiltonians to qubits and Pauli gates
- Algorithms to find ground states, including phase estimation, variational methods, imaginary time evolution, and quantum annealing
- Algorithms for quantum dynamics
- Noise and error mitigation strategies on near-term devices
Prerequisites: PH 125, CH 125 or equivalent graduate quantum mechanics course. ACM 104 or equivalent linear algebra course. Some familiarity with fundamental concepts of quantum computing is beneficial.
Please visit the course webpage, which includes links to class notes.
ACM 270-1 (Spring 2019): Quantum and Classical Information Processes with Tensors
Instructors: Richard Kueng and Joel Tropp
We approach important concepts in quantum and classical information processing from a tensor perspective. We establish a rigorous mathematical framework for tensor calculus and introduce a versatile graphical formalism — wiring diagrams. Subsequently, we apply these ideas to a variety of topics:
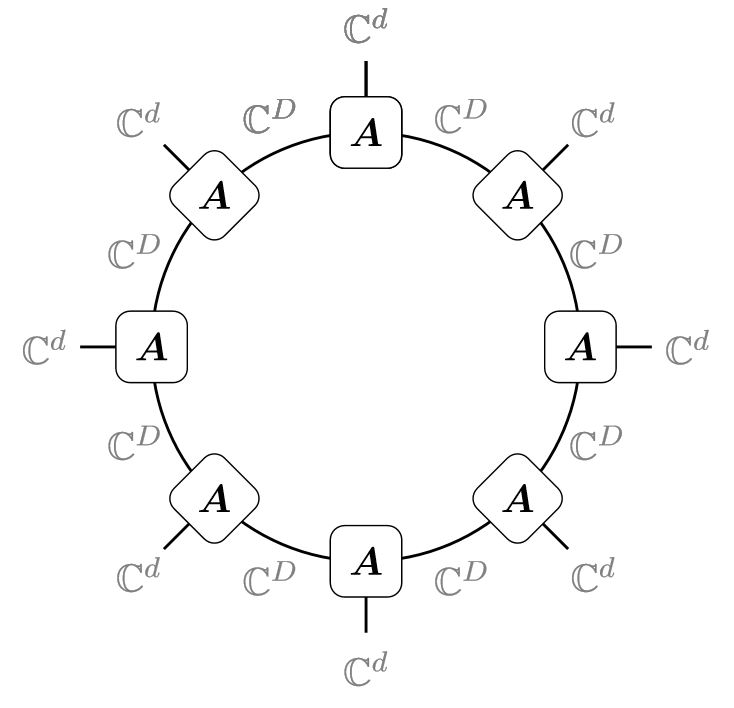
Classical topics
- Determinants and Permanents
- Reversible classical circuits
- Fast matrix multiplication (Strassen plus recent improvements)
- Iterative algorithms for computing useful tensor decompositions (CP and Tucker)
Quantum topics
- Haar integration
- Entanglement
- Quantum circuits
- Tensor trains (matrix product states)
- DMRG
These lecture notes accompany ACM 270-1 at Caltech (spring 2019) — a special topics course aimed at mathematically inclined students from physics, math, computer science and electrical engineering. No quantum background is required, but familiarity with linear algebra is essential.
Courses Related to IQIM Research
Intermediate and Advanced
- Ph 135a Condensed Matter
- Instructor: Motrunich
- Ph 135b Quantum Optics
- Ph/CS 219 a. Quantum Computation
- Instructor: Kitaev
- Ph/APh 223 abc. Advanced Condensed-Matter Physics
- APh 114 abc. Solid-State Physics
- Instructors: Atwater, Schwab
- APh 190 abc. Quantum Electronics
- APh 150 abc. Introduction to Quantum Devices
- Instructor: Painter
Related Topics
- EE/APh 131. Light Interaction with Atomic Systems – Lasers
- Instructor: Atwater
- EE/APh 180. Nanotechnology
- Instructor: Scherer
- APh/MS 105 abc. States of Matter
- Instructors: Johnson, Fultz