Research Highlights and Key Outcomes
2020 Annual Report – IQIM Year 3
IQIM spans Caltech’s departments of physics, applied physics, computer science, electrical engineering, materials science and chemistry. Our program comprises three Major Activities (MAs), organized according to distinct scientific themes rather than experimental platforms, with each MA striking a balance between theory and experiment. The MAs reinforce one another, and much of our scientific success has been derived from the interactions among the groups. Here we report on some of our significant research accomplishments for the past year.
MA-1: Quantum Information Physics
John Preskill, with student Robert Huang and postdoc Richard Kueng, developed an efficient method for finding a succinct classical description of a many-particle quantum state, the state’s “classical shadow,” which can be used to predict accurately many properties of the state. Just log M measurements suffice to predict M different properties, and furthermore the target properties to predict can be selected after the measurements are completed. In numerical experiments, they applied classical shadows to predicting quantum fidelities, entanglement entropies, two-point correlation functions, expectation values of local observables, and the energy variance of many-body local Hamiltonians. The numerical results highlight the advantages of classical shadows relative to previously known methods.
1. Robert Huang, Richard Kueng, and John Preskill, Predicting many properties of a quantum system from very few measurements, Nature Physics 16, 1050 (2020). https://authors.library.caltech.edu/102787/
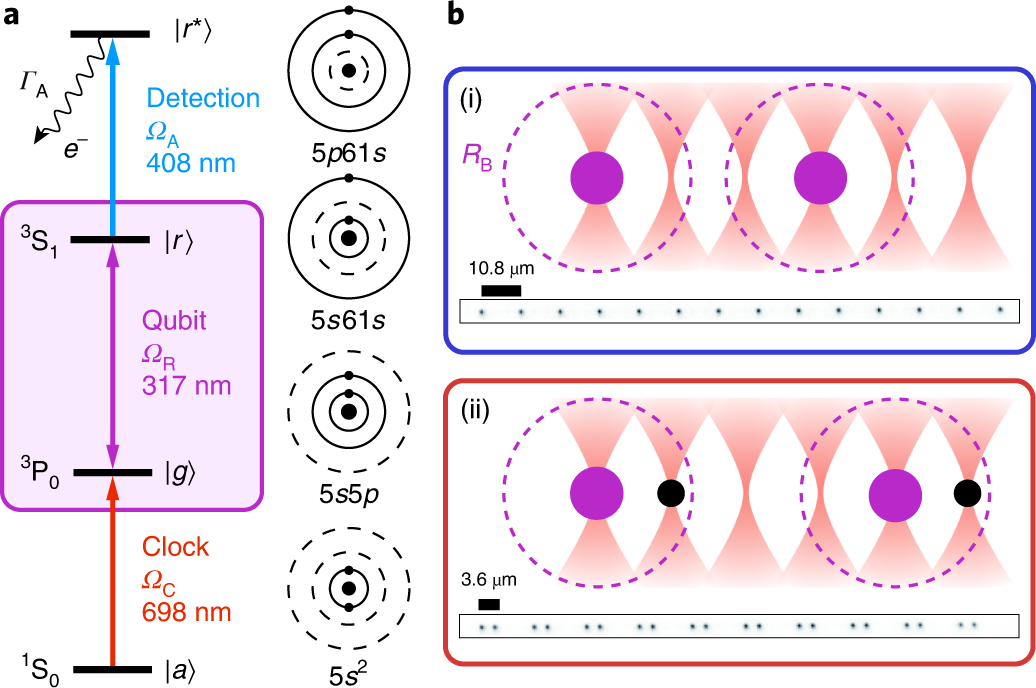
Figure 1: a, The relevant level structure (left) and electronic configuration (right) for strontium-88. The Rydberg ground-state qubit is defined by a metastable ‘clock’ state |g〉 and the 5s61s 3S1 mJ = 0 Rydberg state |r〉 (highlighted with a purple box), which we detect by driving to an auto-ionizing 5p61s state |r*〉. Subscripts: A, auto-ionizing; R, Rydberg; C, clock. The clock state |g〉 is initialized from the absolute ground state |a〉. b, We use atom-by-atom assembly in optical tweezers to prepare an effectively non-interacting configuration ((i), blue box and blue data points throughout) and a strongly Rydberg-blockaded pair configuration ((ii), red box and red data points throughout)7. The blockade radius RB, where two-atom excitation is suppressed, is indicated by a dashed circle. Throughout, purple and black circles indicate |r〉 and |g〉 atoms, respectively. The Rydberg, auto-ionization and clock beams all propagate along the axis of the atom array and address all atoms simultaneously. Averaged fluorescence images of atoms in configurations (i) and (ii) are shown. See Methods and Supplementary Information for further details.
Trapped neutral atoms have become a prominent platform for quantum science, where entanglement fidelity records have been set using highly-excited Rydberg states. However, controlled two-qubit entanglement generation has so far been limited to alkali species, leaving the exploitation of more complex electronic structures as an open frontier that could lead to improved fidelities and fundamentally different applications such as quantum-enhanced optical clocks. Manuel Endres’ group demonstrated a novel approach using the two-valence electron structure of individual alkaline-earth Rydberg atoms. They found fidelities for Rydberg state detection, single-atom Rabi operations, and two-atom entanglement surpassing previously published values. These results pave the way for novel applications, including programmable quantum metrology and hybrid atom-ion systems, and set the stage for alkaline-earth based quantum computing architectures.
2. Ivaylo S. Madjarov, Jacob P. Covey, Adam L. Shaw, Joonhee Choi, Anant Kale, Alexandre Cooper, Hannes Pichler, Vladimir Schkolnik, Jason R. Williams, Manuel Endres, High-fidelity entanglement and detection of alkaline-earth Rydberg atoms, Nature Physics 16, 857 (2020). https://authors.library.caltech.edu/101897/
Thomas Vidick, with IQIM postdocs Anand Natarajan and John Wright and two external collaborators, proved a result in quantum complexity theory that resolves a long-standing open problem in the study of quantum non-locality known as “Tsirelson’s Problem.” Their result shows that two different mathematical methods for formalizing the assumption of spatial isolation that underlies the study of Bell inequalities are not equivalent when entangled states of arbitrarily high dimension are allowed; namely a tensor product of two quantum systems is distinct from a commuting pair of quantum systems. Behind the result lies a dimension test for arbitrarily large entanglement. This result has important consequences in mathematics; in particular, it refutes the celebrated Connes’ Embedding Conjecture in the theory of von Neumann algebras. A remarkable conclusion of their work is that a verifier with access to two provers sharing unlimited entanglement can efficiently check solutions to problems that are undecidable by Turing machines.
3. Zhengfeng Ji, Anand Natarajan, Thomas Vidick, John Wright, and Henry Yuen, MIP*=RE, arXiv:2001.04383 (2020). https://authors.library.caltech.edu/102605/
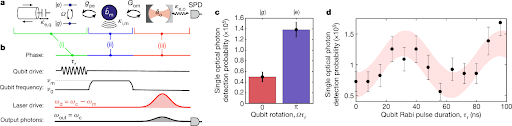
Figure 2: a, b, The pulse sequence for quantum transduction. (i) Electrical drive of varying duration excites the qubit. (ii) The resulting qubit state is swapped to the mechanical resonator. (iii) The mechanical state is read out using a red sideband pulse that converts a phonon at frequency ωm to an optical photon at frequency ωc. The output photons are detected using a single photon detector (SPD; see Methods). c, π-pulse probability Pπ = (1.38 ± 0.14) × 10−5, no-π-pulse probability P0 = (0.50 ± 0.09) × 10−5. d, Qubit Rabi oscillations detected via single optical photon detection. Shaded region shows 90% confidence interval of a sinusoidal fit to the data, with the period of oscillations set to the values from (microwave) dispersive readout of the qubit Rabi curve. Background ((0.67 ± 0.17) × 10−5) and maximum ((1.38 ± 0.17) × 10−5) values from the fit are in agreement with the numbers from c. Error bars in c and d represent the standard deviation at each point, using the raw photon counts and assuming Poissonian shot noise. Measurements performed using an integration time of 38 ns with a 10-ms delay between consecutive pulses (see Methods).
Mohammad Mirhosseini and Oskar Painter, with postdoc Alp Sipahigil and student Mahmoud Kalaee, demonstrated the conversion of a microwave-frequency excitation of a superconducting transmon qubit into an optical photon. They achieved this using an intermediary nanomechanical resonator which converts the electrical excitation of the qubit into a single phonon by means of a piezoelectric interaction, and subsequently converts the phonon to an optical photon via radiation pressure. They demonstrated optical photon generation from the qubit with a signal-to-noise greater than unity by recording quantum Rabi oscillations of the qubit through single-photon detection of the emitted light over an optical fiber. With proposed improvements in the device and external measurement set-up, such quantum transducers may lead to practical devices capable of realizing new hybrid quantum networks, and ultimately, distributed quantum computers.
4. Mohammad Mirhosseini, Alp Sipahigil, Mahmoud Kalaee, Oskar Painter, Superconducting qubit to optical transduction, Nature 588, 599-603 (2020). https://authors.library.caltech.edu/102572/
MA-2: Topological Quantum Physics
Magic-angle twisted bilayer graphene exhibits a range of correlated phenomena that originate from strong electron-electron interactions. In a joint experiment/theory collaboration, the Nadj-Perge and Alicea groups studied topological phases in twisted bilayer graphene in finite magnetic fields. By following the evolution of the local density of states at the Fermi level with electrostatic doping and magnetic field, they visualized a local Landau fan diagram that enabled direct assignment of Chern numbers to all observed phases. They uncovered six distinct topological phases emanating from integer fillings in finite fields, whose origin relates to a cascade of symmetry-breaking transitions driven by correlations. Both the microscopic origin and extreme sensitivity to twist angle differentiate these topological phases from the Landau levels observed near charge neutrality. Their results show how strong electronic interactions lead to the formation of correlation-enabled topological phases in twisted bilayer graphene.
5. Youngjoon Choi, Hyunjin Kim, Yang Peng, Alex Thomson, Cyprian Lewandowski, Robert Polski, Yiran Zhang, Harpreet Singh Arora, Kenji Watanabe, Takashi Taniguchi, Jason Alicea, Stevan Nadj-Perge, Tracing out Correlated Chern Insulators in Magic Angle Twisted Bilayer Graphene, (ArXiv: 2008.11746; Accepted to Nature)
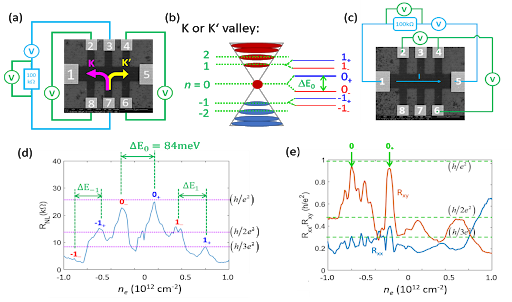
Figure 3: (a) Device configuration for measurements of the non-local resistance (RNL) on a valley Hall transistor made of nanoscale strained graphene (dark color) on SiO2/Si substrate (gray color). A back-gate electrode is attached to the back of Si (not shown), and RNL is measured by applying currents across contacts 3-7 and measuring the voltage across either 2-8 (for K-valley) or 4-6 (for K′-valley). (b) Schematics for quantized energy levels associated the PMF-induced Landau levels (n: Landau level index) at one of the Dirac cones and further energy splitting due to strong Coulomb interaction-induced spontaneous symmetry breaking & spin polarization. (c) Device configuration for measurements of anomalous Hall resistance (Rxy) across either 2-8 or 4-6 by applying current across 1-5. (d) RNL–vs.-ne results under the configuration in (a) at 1.8 K, showing quantized energy levels and quantum valley-Hall resistance. (e) Rxy–vs.-ne data under configuration in (b) at 1.8 K, showing quantum anomalous Hall resistance.
Nai-Chang Yeh’s group recently developed a new way to tune electronic correlations and band structures in van der Waals (vdW) materials by means of quantum straintronics: nanoscale strain engineering of monolayer vdW materials achieved by depositing the monolayer on designed arrays of nanostructures. In monolayer graphene, scanning tunneling spectroscopy as well as Raman spectroscopy confirmed the effects of nanoscale strain and the formation of giant pseudo-magnetic fields. They also patterned the strained graphene into a valley Hall transistor. Their observations of energy shifts in the strain-induced Landau levels are consistent with strong spin polarization in the strained graphene. These new findings may pave the way for the fractional quantum value Hall effect and for Harper-Hofstadter bands associated with the fractional Chern insulators, as well as other correlated topological phases, and may eventually lead to devices such as dissipationless field effect transistors (FETs), and new robust qubit architectures.
6. C.-C. Hsu, M. L. Teague, J.-Q. Wang, and N.-C. Yeh, Nanoscale Strain Engineering of Giant Pseudo-Magnetic Fields, Valley Polarization and Topological Channels in Graphene, Science Advances 6, eaat9488 (2020), DOI: 10.1126/sciadv.aat9488
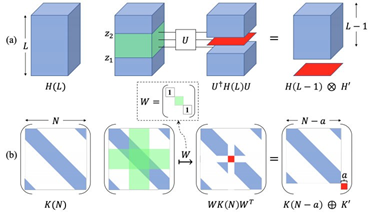
Figure 4. Foliated fracton order and its interpretation in terms of K matrix. In Figure (a) (first line), we start with a system H(L) of size L in the z direction. A finite depth local unitary circuit U is applied to the green region {(x, y, z) : z1 ≤ z ≤ z2}. The result is the same system H(L−1) of size L−1 in the z direction and a decoupled 2+1D gapped system (red layer). In Figure (b) (second line), we start with a quasi-diagonal K(N) of size N ∝ L with periodic boundary condition. Only entries in the blue region can be non-zero. We apply the transformation K(N) 7→ WK(N)WT , where W ∈ GL(N, Z) shown in the dashed box is equal to the identity except in the green block, so the action of W on K(N) is within the green cross in the second figure. The result is the direct sum of the same system K(N − a) of size N − a and a decoupled block K0 of size a = O(1) (red block)
Fracton models embody a new class of exotic topological phenomena that is yet to be understood within the condensed matter theory framework. Previous work in Chen’s group on this topic – in particular the identification of a foliation structure in fracton models – was mostly based on the study of exactly solvable models, which quickly became too complicated to work with beyond the simplest ones. In the past year, Chen’s group has worked on using field theoretical tools to study gapped fracton phases. It was shown in [3] that the Chern-Simons (CS) gauge theory can provide a powerful tool for this purpose. In 2+1D, the CS gauge theory played an important role in describing topological phases. It was realized in [3] that by extending the 2+1D CS gauge theory to contain an infinite component of gauge fields, it can describe 3+1D gapped fracton order. Interestingly, it was found that, such a framework goes beyond the exactly solvable one in a significant way – it led to the identification of type I fracton models without a foliation structure, which had not been possible with exactly solvable models.
7. Xiuqi Ma, Wilbur Shirley, Meng Cheng, Michael Levin, John McGreevy, Xie Chen, Fractonic order in infinite-component Chern-Simons gauge theories, arXiv:2010.08917.
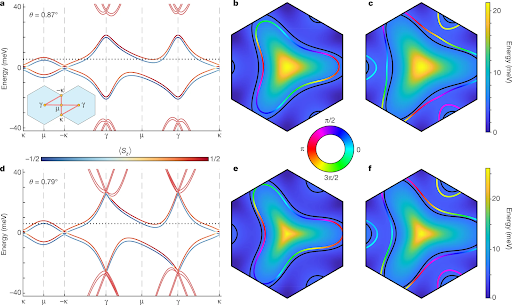
Figure 5: a-f | Continuum-model results for valley K that include Ising and Rashba spin-orbit coupling at twist angles of 0.87º (a-c) and 0.79º (d-f). Details are given in Methods and Supplementary Information section 1. a, d, Band structure along the high-symmetry directions of the Brillouin zone, as indicated in the inset. The line color represents the out-of-plane spin projection, <S7>, and the dotted horizontal line denotes the chemical potential corresponding to v = +2. b, c, e, f, Energy of the upper pair of flat conduction bands, including spin-orbit coupling. Colored lines show the Fermi surfaces at v = +2, with the color indicating the in-plane spin projection. The out-of-plane projection is largely constant along these surfaces and may therefore be deduced from a and d. Black lines correspond to the Fermi surface with SOI effects. The large spin-orbit-coupling-induced Fermi-surface deformation visible here reflects the flatness of the bands near the Fermi energy. The persistence of superconductivity with such distortions constrains the probable pairing channels in TBG. We note that the apparent electron-hole symmetry in the band structure is a consequence of the twist angle being well below the magic angle.
Twisted bilayer graphene has been shown to host a spectacularly rich phase diagram featuring correlated insulators and superconductivity. In a joint experiment/theory collaboration, the Nadj-Perge and Alicea groups studied for the first time twisted bilayer graphene supported by WSe_2, which imparts strong spin-orbit interaction to the graphene layers. Remarkably, superconductivity not only survives but thrives in the presence of spin-orbit coupling—persisting over a much broader window of twist angles compared to previously studied devices. These observations strongly constrain the nature and origin of superconductivity in twisted bilayer graphene, while additionally illuminating a tantalizing new pathway to device engineering.
8. H. S. Arora, R. Polski, Y. Zhang, A. Thomson, Y. Choi, H. Kim, Z. Lin, I. Z. Wilson, X. Xu, J.-H. Chu, K. Watanabe, T. Taniguchi, J. Alicea, S. Nadj-Perge, Superconductivity in metallic twisted bilayer graphene stabilized by WSe₂, Nature 583, 379 (2020); highlighted in News and Views by Ronny Thomale. [arXiv:2002.03003] https://authors.library.caltech.edu/101531/
MA-3: Quantum Dynamics
![Ultrafast optically induced enhancement of ferromagnetic exchange [9], Figure 6](https://iqim.caltech.edu/files/2021/02/Ultrafast-optically-induced-enhancement-of-ferromagnetic-exchange-9-Figure-6.png)
Figure 6: (a) Temperature dependence of the second harmonic generation signal from CrSiTe3, which was previously shown to track the spin-spin correlator. Spin correlations markedly increase below T2D ∼ 110 K and then diverge at Tc = 33 K when long-range order sets in. (b) Temperature dependence of time-resolved reflectivity transients from CrSiTe3 showing an oscillatory component arising from coherent oscillations of a totally symmetry Ag3 phonon. The pump photon energy is resonant with the charge transfer transition. (c) Temperature dependence of the Ag3 phonon oscillation phase (top) and amplitude (bottom) extracted from the transient reflectivity data. The 180° phase flip below T2D is evidence of a charge transfer transition induced enhancement of the superexchange interaction.
David Hsieh and Gil Refael theoretically predicted and experimentally demonstrated a nonthermal pathway to optically enhance superexchange interaction energies in a material based on exciting ligand-to-metal charge-transfer transitions. The mechanism works by introducing lower-order virtual hopping contributions that are absent in the ground state. They demonstrated this effect in the layered ferromagnetic insulator CrSiTe3 by exciting Te-to-Cr charge-transfer transitions using ultrashort laser pulses and detecting coherent phonon oscillations that are impulsively generated by superexchange enhancement via magneto-elastic coupling. This mechanism kicks in below the temperature scale where short-range in-plane spin correlations begin to develop and disappears when the excitation energy is tuned away from the charge-transfer resonance, consistent with their predictions.
9. A. Ron, S. Chaudhary, G. Zhang, H. Ning, E. Zoghlin, S. D. Wilson, R. D. Averitt, G. Refael, and D. Hsieh, Ultrafast Enhancement of Ferromagnetic Spin Exchange Induced by Ligand-to-Metal Charge Transfer, Phys. Rev. Lett. 125, 197203 – Published 4 November 2020 https://authors.library.caltech.edu/100322/
Gil Refael, Or Katz and former IQIM postdoc Netanel Lindner examined the effects of strong optical driving on twisted bilayer graphene near magic twist angles. As already discussed in the context of MA-2, the undriven system features flat electronic bands, which lead to strongly correlated superconducting and topological physics. In equilibrium, these exotic properties are typically limited to a narrow range of twist angles around the magic angle with a small allowed tolerance. Katz, Refael and Lindner predict an alternative mechanism that enables band flattening using coherent optical illumination, leading to emergence of flat isolated Floquet-Bloch bands. They showed that the effect can be realized with relatively weak optical beams in the visible-infrared range (below the material bandwidth) and persist for a wide range of small twist angles, increasing the allowed twist tolerance by an order of magnitude. These optically induced flat bands could potentially host strongly-correlated, nonequilibrium electronic states of matter with non-trivial topology.
10. Or Katz, Gil Refael, and Netanel H. Lindner, Optically induced flat bands in twisted bilayer graphene, Phys. Rev. B 102, 155123 – Published 16 October 2020 https://authors.library.caltech.edu/106127/
The energy damping time in a mechanical resonator is critical to many precision metrology applications, such as timekeeping and force measurements. Mohammad Mirhosseini and Oskar Painter’s groups explored the use of high-quality microresonators in which the acoustic environment can be engineered, extending the phonon lifetime to more than 1 second. These acoustically engineered nanoscale structures provide a window into the material origin of quantum noise and have potential applications ranging from tests of various collapse models of quantum mechanics to miniature quantum memory elements in hybrid superconducting quantum circuits.
11. Gregory S. MacCabe, Hengjiang Ren, Jie Luo, Justin D. Cohen, Hengyun Zhou, Alp Sipahigil, Mohammad Mirhosseini, Oskar Painter, Nano-acoustic resonator with ultralong phonon lifetime, Science 370, 840-843 (2020), https://authors.library.caltech.edu/106664/
Gil Refael, Thomas Rosenbaum, and Daniel Silevitch, with postdoc Michael Buchhold and graduate student Christopher Tang, developed a model to treat the nonlinear dynamics of clusters of dipole-coupled spin systems. The theory illuminated experimental results on the highly-disordered Ising spin system LiHo0.045Y0.955F4 with respect to the emergence of highly coherent (Q ~ 105) Fano resonances when the system is pumped with a strong ac magnetic field. The observations can be understood in terms of a Lambda energy level scheme of a cluster of spins, solved analytically for n = 2 and 3, and numerically for n up to 12. In the presence of an increasing number of spins, the resonances arise from interference between manybody quantum spin levels and can be observed at surprisingly low energies and driving frequencies. The crucial requirement for its observation at low frequencies is, however, dissipation rates, i.e., phonon lifetimes, which are of the order of the driving frequencies or even smaller. These results pave the way for further studies of the emergence of quantum effects in strongly diluted and strongly frustrated Ising spin systems and of their low-energy, non-equilibrium phase diagrams.