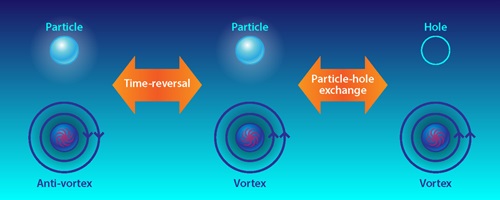
Credit: APS/Alan Stonebraker
Figure 1: The action of discrete symmetries on the fermionic particle (top) and its dual fermionic vortex (bottom).
In a new paper by IQIM Postdoctoral Scholar David Mross together with Jason Alicea and Lesik Motrunich they explicitly derive the duality between a free electronic Dirac cone and quantum electrodynamics in (2+1) dimensions (QED3) with N=1 fermion flavors. The duality proceeds via an exact, nonlocal mapping from electrons to dual fermions with long-range interactions encoded by an emergent gauge field. This mapping allows them to construct parent Hamiltonians for exotic topological-insulator surface phases, derive the particle-hole-symmetric field theory of a half-filled Landau level, and nontrivially constrain QED3 scaling dimensions. They similarly establish duality between bosonic topological insulator surfaces and N=2 QED3. Read the paper Phys. Rev. Lett. 117, 016802 (2016) published June 27, 2016 – Explicit Derivation of Duality between a Free Dirac Cone and Quantum Electrodynamics in (2+1) Dimensions
The paper is featured in a Physics – Viewpoint: Fermionic Vortices Find their Dual “Dirac fermions in 2+1 dimensions (two spatial dimensions plus time) have been found in graphene and on the surfaces of topological insulators (TIs). A trio of papers now shows that these particles can also be found in a dual description of quantum electrodynamics (QED). This deceptively simple statement joins together several disparate lines of progress in theoretical physics: interacting topological insulators, anomalies in quantum field theory, spin liquids, and compressible quantum Hall states.”
The viewpoint also references a recent paper by IQIM alumni Scott Geraedts working with Roger Mong, Motrunich and other collaborators “The Half-Filled Landau Level: The Case for Dirac Composite Fermions,” Science 352, 197 (2016)



