John Preskill and former IQIM Postdoctoral Scholar, Fernando Pastawski present new work in Code Properties from Holographic Geometries Phys. Rev. X 7, 021022 (2017). An overview is presented in the paper’s Popular Summary:
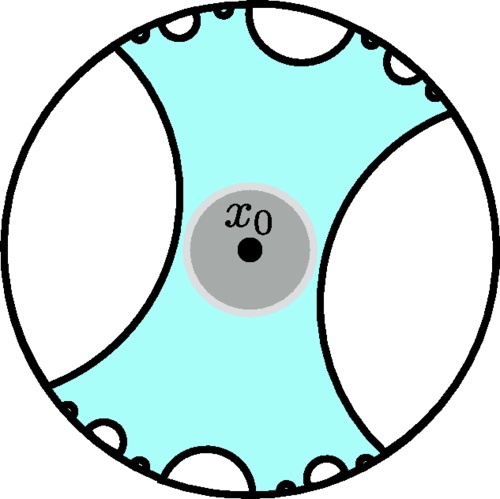
This figure illustrates uberholography for the case of a two-dimensional hyperbolic bulk geometry. The inner logical boundary is contained inside the entanglement wedge, shaded in blue, of a boundary region R. By repeatedly punching holes of decreasing size out of this boundary region, we obtain a much smaller region Rmin whose entanglement wedge still contains the logical boundary. Thus, the logical algebra is supported on a fractal boundary set, whose geometry is reminiscent of the Cantor set. Fig 5 from the paper.
A deep link might exist between two seemingly disparate but far-reaching ideas in physics: quantum error correction and the holographic principle. Quantum error correction concerns using redundant encoding to protect quantum information from damage, and it has been studied extensively because of its relevance to reliable operation of noisy quantum computers. The holographic principle, meanwhile, states that all information about a volume of space can be encoded on the surface area of that volume, much as a hologram encodes a 3D image on a 2D surface. Recent research suggests that how our physical space is structured may also correspond to redundantly represented information. We further explore this connection between redundant information and geometry.
Specifically, we look at connections between quantum error-correcting codes and the “holographic correspondence,” which asserts that a suitably chosen quantum theory, without gravity, can be precisely equivalent to a theory of quantum gravity in a negatively curved spacetime. We analyze the properties of holographic quantum codes, quantum error-correcting codes that capture the essential features of the holographic correspondence. These codes provide an information-theoretic interpretation for physical notions such as points in space, black holes, and spacetime curvature.
Our work provides a new paradigm for designing quantum error-correction schemes and secret sharing codes, from which we expect many new constructions, and it also clarifies the information-theoretic foundations of the holographic correspondence.
Read the full paper Pastawski, Fernando and Preskill, John (2017) Code Properties from Holographic Geometries. Physical Review X, 7 (2). Art. No. 021022. ISSN 2160-3308.



